Installation
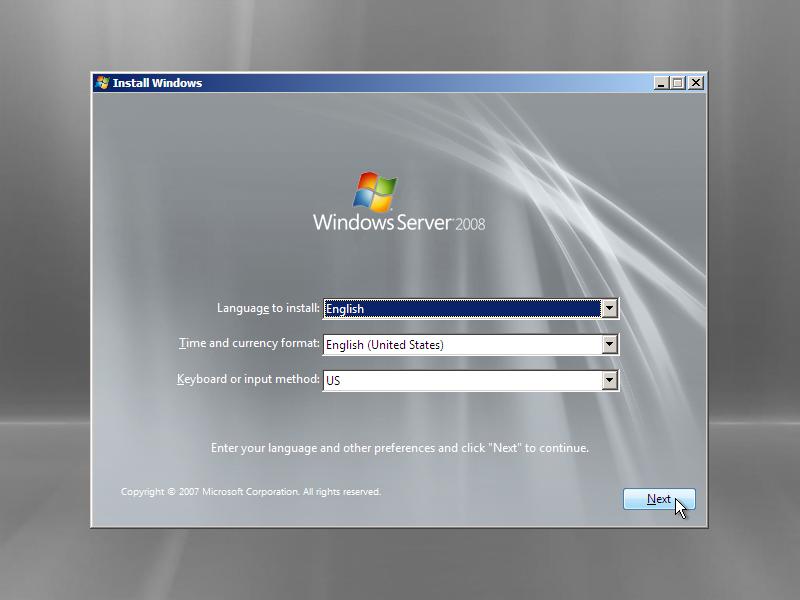
1. Boot up your Windows Server 2008 dvd. If you see the screen below, choose the approperiate settings and click Next.
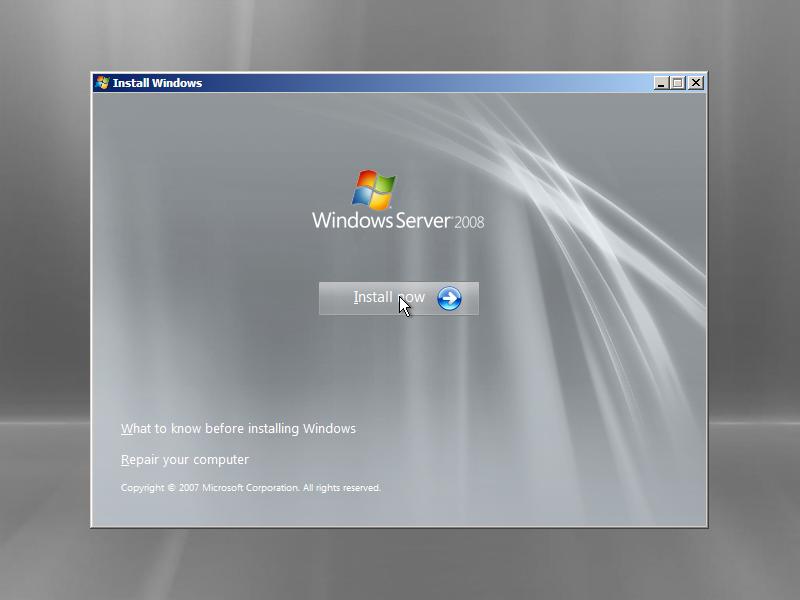
2. On the next screen just click the button Install Now.
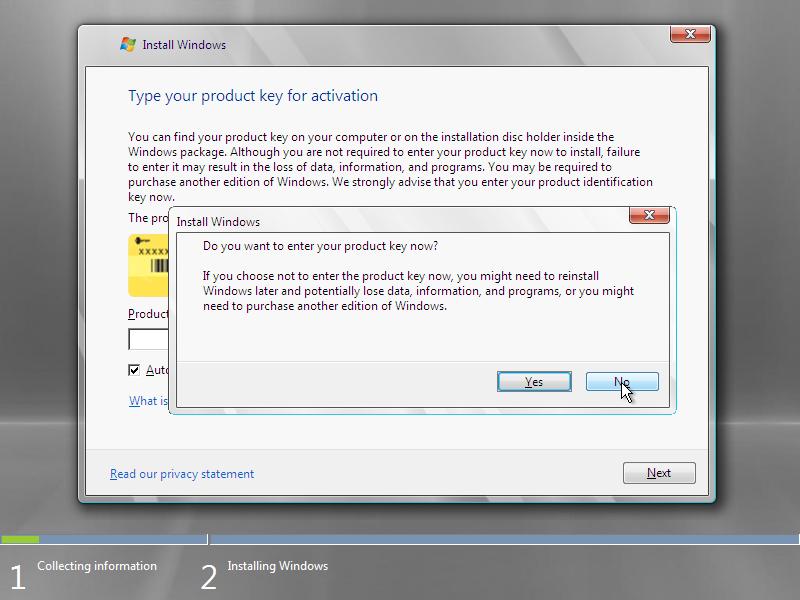
3. Enter your Windows Server 2008 productkey. If you don’t have one (yet) you can just skip this step by clicking Next and click No when asked when asked if you want to enter your product key.
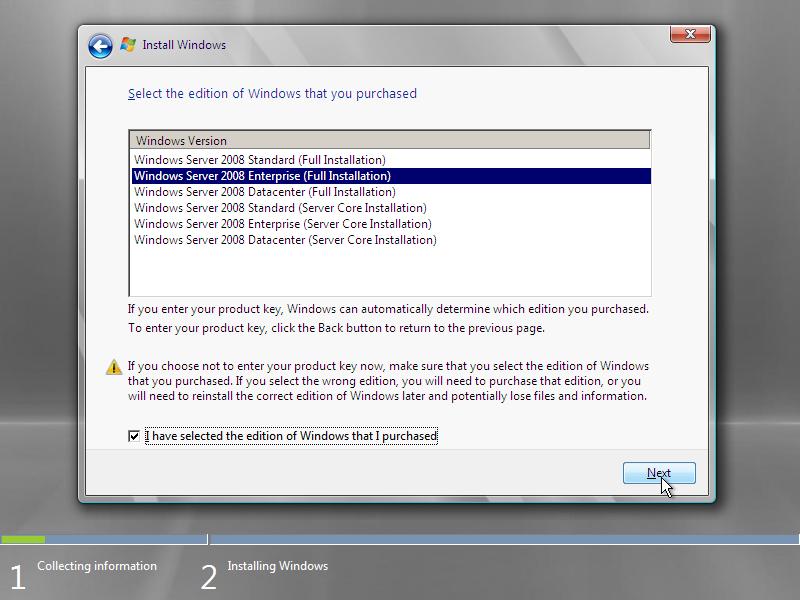
4. Select the version of Windows Server 2008 that says Full Installation. Don’t select one of the Server Core Installation’s, because then you won’t have a GUI 😉
5. If you agree to the license terms, select I accept the license terms and click Next.
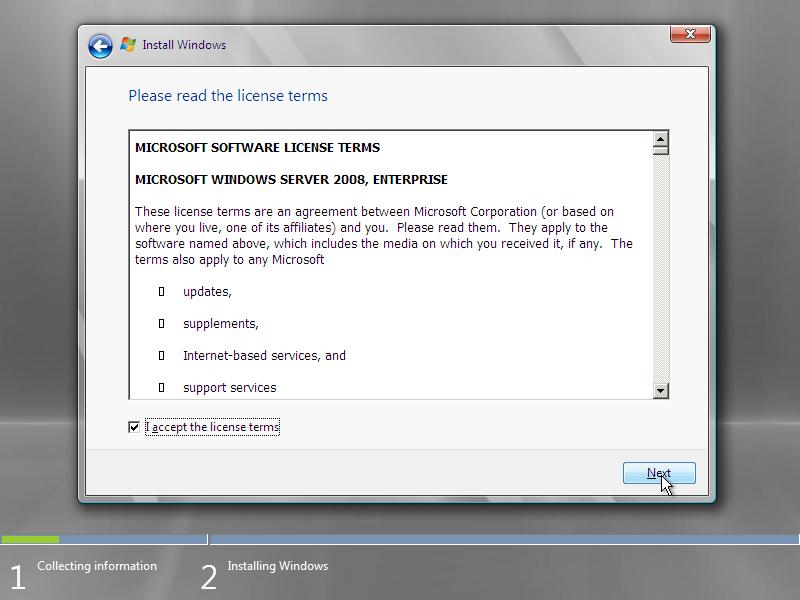
6. If you have a clean harddisk or if there is no possibility to upgrade from a previous version of Windows you will only have the option Custom (advanced). In this manual I will use the Custom installation.
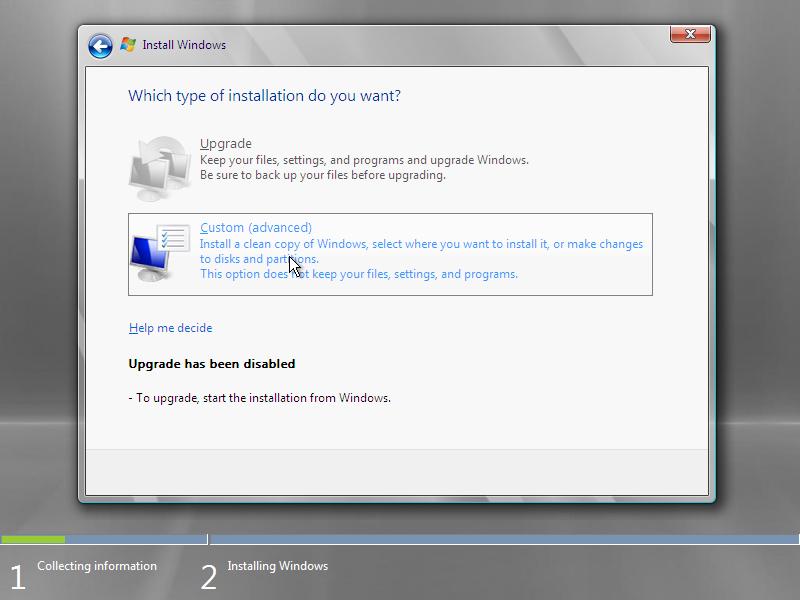
7. Select the harddisk and partition where you want to install Windows Server 2008 and click Next.
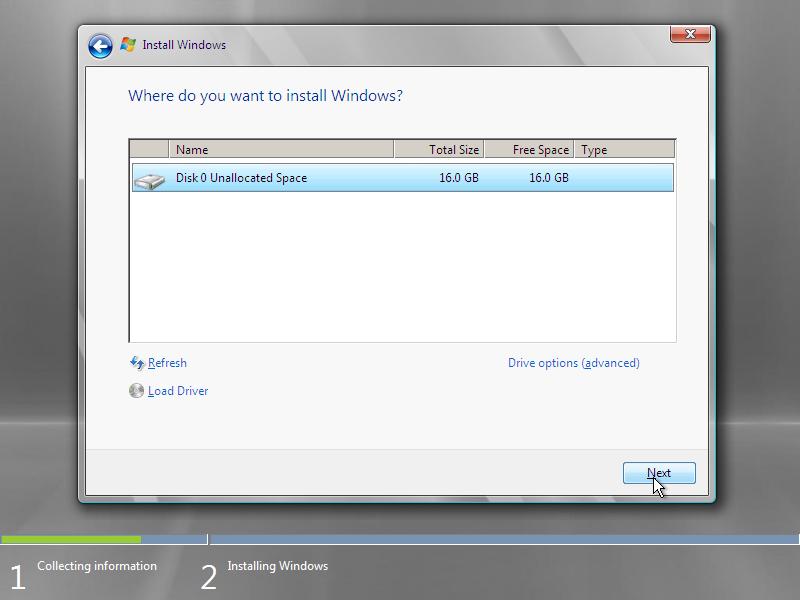
8. Now Windows 2008 Server setup will install the selected version on your harddrive.
9. After the installation has finished the computer will restart and a message about changing your password will be shown. Click OK.
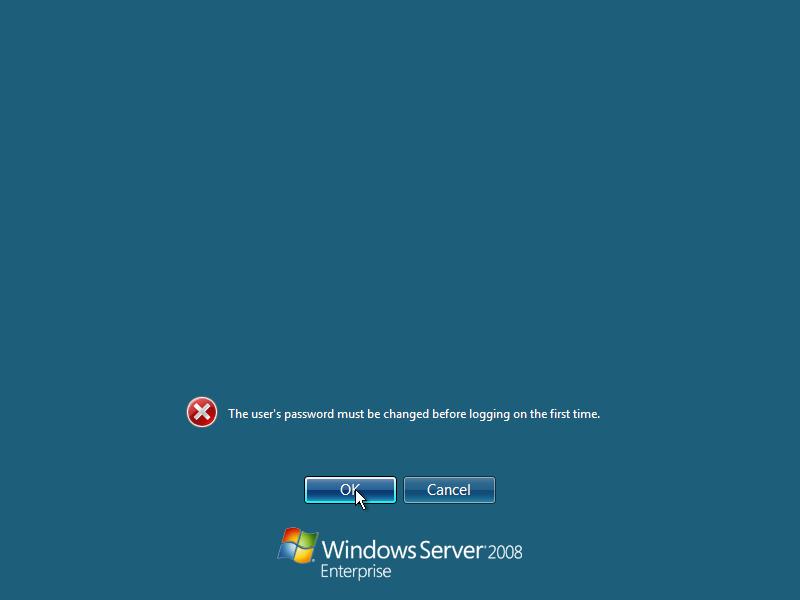
10. You MUST type in a strong password with at least one capital letter and one number, for example P4ssword (capital P/number four), otherwise you will get an error message saying that you doesn’t comply to the security enforcements of the domain. You can disable this strong password enforcement later. After succesfully changing the password you will see the message that your password has succesfully been changed. Click OK. Your desktop will now show up.
11. In the Server Manager window check the Do not show me this console at logon to not show the Server Manager at startup. You can access it later via the the Server Manager shortcut in your quick launch bar or Start menu.



I am microsoft system Administrator I learn server 2003 but now i want upgrade to server 2008 i need server 2008 step by step installation.
😥
Depois de reiniciar obtive o erro:(English please) After reboot I got the error:Problem signature:
Problem Event Name: CLR20r3
Problem Signature 01: oobe.exe
Problem Signature 02: 6.0.6001.18000
Problem Signature 03: 47917825
Problem Signature 04: Microsoft.Windows.ServerManager
Problem Signature 05: 6.0.0.0
Problem Signature 06: 49e037dd
Problem Signature 07: 1f31
Problem Signature 08: 0
Problem Signature 09: System.NullReferenceException
OS Version: 6.0.6002.2.2.0.256.1
Arris: There is a topic about this issue at the Microsoft Forums.
Thanks for the evry easy to follow instructions with the screen shots
Arris: You’re welcome! 🙂
It is really good to watch.
Even a common person can also install OS by using the above screen shots
i am followed the same your above instructions but i am facing some problem.
after the installation drivers show two time in my computer like.,
c: windows,
c: windows
d: local disk
d: local disk
Please assist me how to sorted out the issues.
Cheers
Senthil Kumar.M
Arris: I’ve never seen such problem, maybe someone at the forum can help you.
I have the same error above,any solution
I have this error on my computer after finishing the above setup. Actually i have no way to fix this yet.
I cannot install domain controller because of this error.
==================
Description:
Stopped working
Problem signature:
Problem Event Name: CLR20r3
Problem Signature 01: oobe.exe
Problem Signature 02: 6.0.6001.18000
Problem Signature 03: 47917825
Problem Signature 04: Microsoft.Windows.ServerManager
Problem Signature 05: 6.0.0.0
Problem Signature 06: 49e037dd
Problem Signature 07: 1f31
Problem Signature 08: 0
Problem Signature 09: System.NullReferenceException
OS Version: 6.0.6002.2.2.0.256.1
Locale ID: 1033
Read our privacy statement:
http://go.microsoft.com/fwlink/?linkid=50163&clcid=0x0409
Cant get past the liscense key page i press next and no on the popup and it freezes, left it for over an hour and tried restarting a few times, it still wont get past that page
Thanks in advance -pmp
ON the fact of the CHANGE PASSWORD at first startup up , by default windows server is set to complex password level meaning you need to provide a password with
1-letters
2-numbers
3-symbols
it only obvious that one who actually had experience in a administrating a server would anticipate this type of security
Windows Sever 2008 can run smoothly on Pentium 4 machines with as little as 256 megs or even less (with some tuning and pruning). It should have 512 megs during installation though.
I’m having Vista Home Premium on my 64-bit computer. Now I want install W2K8 Enterprise in parallel. After reaching your step
“8. Now Windows 2008 Server setup will install the selected version on your harddrive.” the installation process begins. In the second installation step “Expanding files” after about 20% a re-boot occurred and after this a BSOD appeared. My investigation result is: some drivers are missing. So I tried in your step
“7. Select the harddisk and partition where you want to install Windows Server 2008 and click Next.” to load the drivers but how can this be done? I was not able to use the Vista drivers. It seems that the installed Vista drivers are not in the original state. But Vista works fine. So, I then downloaded the drivers (I think ..), but W2K8 stated that I should use 32-bit drivers and signed 64-bit drivers; I couldn’t continue. Can you help how I could proceed?
My computer is a “Packard Bell IMEDIA X7600 GE”,
the installation process recognized the drivers as correct, but refuses them afterwards.
The harddisks are “WDC WD10 EAVS-00D7B1 SCSI Disk Device”.
I used drivers in Vista “NVIDIA nForce Serial ATA Controller”.
Arris: I currently don’t have any clue to solve this problem. Maybe you can post this question at the Win2008Workstation Forums or the Microsoft Technet Forums to get a solution.
HI!! I installed but I cannot activate it. it gives me an error and cannot be activated. Is anyone who knows why?
Arris: Try to activate it by phone. See this page for the list of phone numbers.
Problem solved. Just make sure all peripherals are disconnected when you install.
Hi Arris,
Great article. I’m not a Technet subscriber so I can’t post there but I can’t install Server 2008 x64. I get the following message;
Windows failed to start…
File: windowssystem32bootwinload.exe
Status: 0xc0000001
Info: The selected entry could not be loaded because the application is missing or corrupt.
I get this same message even when I install directly from the iso into a virtual machine or from a disk on to bare metal. I’ve also tried downloading the same file twice but get the same result each time.
Any ideas? I’d appreciate your input as I am frustratedly looking for a useable, stable work machine. Vista is too bloated for me and I’ve wasted 2 months on Linux. I did run Windows Server 2003 R2 as a workstation briefly in the past and that seemed perfect except it won’t run with my new hardware.
thanks in advance – and thanks for a helpful website
Arris: I believe everyone with a Windows Live ID can post messages at the Technet Forums. However, to fix your problem you might try the method described at the forum: dual boot with XP.
Anyone upgrade to R2 yet ?
Great article!
I have Win Server 2008 Enterprise running on my Dell Inspiron 6400.
There are a few driver issues, but apart from that, it’s great 🙂
Thanks for the guide
Arris: Good to hear that! Thanks for your comment. 🙂
I have this error on my computer after finishing setup. Actually i have no way to fix yet.
I cannot install IIS because of this error.
==================
Description:
Stopped working
Problem signature:
Problem Event Name: CLR20r3
Problem Signature 01: mmc.exe
Problem Signature 02: 6.0.6001.18000
Problem Signature 03: 47918d09
Problem Signature 04: Microsoft.Windows.ServerManager
Problem Signature 05: 6.0.0.0
Problem Signature 06: 4791a748
Problem Signature 07: 1f26
Problem Signature 08: 1f
Problem Signature 09: System.NullReferenceException
OS Version: 6.0.6001.2.1.0.256.1
Locale ID: 1033
Read our privacy statement:
http://go.microsoft.com/fwlink/?linkid=50163&clcid=0x0409
==================
hey, i’m sorry, i had found this post through a search engine, not through the host site, and i just discovered this is part of a huge well-written, extensive walk-through on exactly what i’ve been doing for the last two days, so i withdraw the more critical parts of my previous post…seriously, sorry about that, i shoulda looked around a bit more before posting.
but really, nice job on the whole thing 🙂
Arris: No problem! I understand! 😉 Thanks for the compliments and good luck tweaking your Server 2008. 🙂
umm…what the hell is the point of posting this?
if you need an online walk-through on how to install a windows os, then the one you install probably shouldn’t be windows server 08.
when i installed server08, i researched the default password policy requirements, pasted here (unfortunately i lost the bookmark for the quoted site, as i saved the quote as text, but i believe it was from thebackroomtech.com):
-Passwords cannot contain the user’s account name or parts of the user’s full name that exceed two consecutive characters.
-Passwords must be at least six characters in length.
-Passwords must contain characters from three of the following four categories:
-English uppercase characters (A through Z)
-English lowercase characters (a through z)
-Base 10 digits (0 through 9)
-Non-alphabetic characters (for example, !, $, #, %)
(end quote)
i took my standard password (7 lowercase letters, plus a numeral), and added ‘.’ (a period) at the end; made it still fairly natural to type, met the criteria, and it’s a small adjustment for me to make from what i’m used to typing. i only mention this because if you guys are talking about this stuff, you’re probably the kind of user who tends to type passwords from muscle memory, and hate having to change your pattern, me too, makes me furious.
and don’t get me wrong, these are very clear and well written instructions (so good job, and kudos on that), but i just think it’s ironic that such a basic topic for a walk-through as installing an os, is required for the most advanced windows os available.
At step 10, when you enter the admin password (twice) there is an option to create a password reset (to blank) file. You can do this to a USB drive (file size is like 2K).
You then go to “Initial Configuration Tasks” (set time / date, time zone, computer name, etc.). Here you can also check a box not to show this dialog window at start-up.
Overall, these notes (and the rest of your instructions) are VERY good
I get a black screen with gray letters:
a Hardware error.
and then i need to put in a installation disk. but that disk is mounted,
its coming back all the time
Arris: I think you ‘d better ask this question in the Windows Server 2008 Section at the Microsoft Technet Forums. There are lots of geeks there that can help you! 🙂
R. Vail – Fixed my HP XW6600 by going to BIOS and changing from RAID to IDE. If you don’t you will need to create a floppy with the Sata Raid drivers to use during install.
Admin: Thanks for putting this info together!
Thanks, this worked out…!!!
Can you really skip the license key screen and get away with it??
Arris: That’s right, it is possible to skip the license key screen and enter your license key later in Windows. Same is possible in the Windows Vista setup.
Check the media if something fails. The first DVD I burned did give a generic error. After reburning, the installation went smoothly.
I couldn’t install on Raid-0 as well, installed on SATA/IDE and try to migrate to RAID later on. And had to start over when I tried to add the Nvidia drivers. Blue screens pops up and I could start over again 🙁
Awesome guide! It has been really useful.
Thanks.
Arris: Thanks for the compliments. 🙂 If you have ANY questions, don’t hesitate to ask them at the forums!
I’m having issues installing Windows 2008 on a machine. (A Server)
Dual Xeon 3.0GHz, 6 Gig, “C” RIAD 0 – 120G sATA and Data “D” drive RAID 5(4x400G – sATA drive – Custom Built server.
When it comes to expending files – it goes upto 18%, 10% and just few % and will not go further. I’ve tried with less memories, pulled RAID 5 drives out but nothing works. I have someone else tried on their home computers and it works. DVD/CD are good. Your recommandation and help would be greatly appreciated. Thanks.
Arris: I have no idea what the problem can be. You can try to find a solution at the Microsoft Technet Forums in the Windows Server : Setup Deployment section or create a thread there so other Microsoft Professionals can help you. Good luck!
There are few different version of 2008 server. What one did you use? Or what would you recommend.
Arris: Here is a topic about the different versions of Windows Server 2008. I am currently using the x64 Enterprise because it’s the most extended version that includes Hyper-V.
Gee! It would be nice to have that kind of money to blow for a copy of Windows Server 2008, esp. since I got my Vista for nothing.
Just had a look at this. Looks awesome. Will try this if my Win XP x64 fails – and this might be only a few weeks away as i’m willing to destroy it over and over again…..
Thanks. 🙂
I’m downloading it now.
It worked like a charm ! thx for the tip this is much better then plain Vista !!
Thanks for this guide! I am now tri-booting Windows Server 2008, Mac OS X 10.5, and Ubuntu 8.04 on my MacBook Pro.
Yes! 😀 It is working fine om my laptop now! Thanks for this great manual!
@m.oreilly
Like already said by Admin, the following examples (Passw0rd or P4ssword or P4ssw0rd or P@ssw0rd) work fine.
Valorisa
come installare languace pack italian file *.cab
Grazie
For some reason, I can’t boot from an optical disc when the bios is set to Raid mode. Abit still has not fixed the following bios error (running v. 16 b10):
When attempting to boot from a SATA DVD-RW drive connected to either Intel or JMicron SATA port, bootable optical discs cannot boot when the Intel Raid/IDE/AHCI bios selector is set in Raid mode. Switch back to IDE mode, and the optical disc becomes bootable again.
Anyone else encountered this? I ran into this, when the board was newly released about 9 months ago. A workaround solution is: use the set of (6) WinXP SP2 bootable floppies, in order to install onto a Raid 0 pair of hard drives.
Does MS offer a set of bootable floppies for installing Server 2008 (either: x32 or x64 version?)
i installed it on Parallels for mac….never asked me for a password.
I’ll try to make it more cleer…
Capitalizing the first letter in your password…..and make sure there are letters and numbers in the password….so that its “complex” enough for microsofts standards.
Good Luck!
it won’t get past the stupid password screen. i just spent an hour trying different combinations. a feckin waste of my day, as now i have to reinstall 03…
Arris: I added the remark to step 10 that you *must* enter a strong password, otherwise you can’t log in!